入门可以参考https://morvanzhou.github.io/tutorials/data-manipulation/np-pd/
先占个坑
20180920开始填坑
Numpy:提供了一个在Python中做科学计算的基础库,重在数值计算,主要用于多维数组(矩阵)处理的库。用来存储和处理大型矩阵,比Python自身的嵌套列表结构要高效的多。本身是由C语言开发,是个很基础的扩展,Python其余的科学计算扩展大部分都是以此为基础。
- 高性能科学计算和数据分析的基础包
- ndarray,多维数组(矩阵),具有矢量运算能力,快速、节省空间
- 矩阵运算,无需循环,可完成类似Matlab中的矢量运算
- 线性代数、随机数生成
import numpy as np
ndarray 多维数组(N Dimension Array)
NumPy数组是一个多维的数组对象(矩阵),称为ndarray,具有矢量算术运算能力和复杂的广播能力,并具有执行速度快和节省空间的特点。
ndarray拥有的属性
- ndim属性:维度个数
- shape属性:维度大小
- dtype属性:数据类型
维度
来源:https://blog.csdn.net/Exziro/article/details/78152621
在数学上我们说维度是什么呢?–在一定的前提下描述一个数学对象所需的参数个数。但是我们今天所谈到的维度却和这里数学所说的维度有着一些区别。有标题可知,我们今天所要说的维度是基于numpy中的多维数组。numpy最重要的一个特点就是其N维数组对象,该对象是一个大的灵活的大数据集容器。以此利用数组来对我们获取到的整块的数据执行一些数学上的运算。绕了一圈,维度又是啥,我们先来看一下以下的代码。
> data = np.array([[1,2],[4,5]]) > data.shape() (2L, 2L) > data1 = np.array([[1,2,3],[4,5,6],[7,8,9]]) > data1.shape (3L, 3L)
对人来说高维空间是很难想象的,但是我们可以从纯数学的角度来看。对多维数组来说,确定最底层的一个基本元素位置需要用到的索引个数即是维度。用上面的数组data来举一个简单的例子。当我们要获取 1 的值,我们需要使用 a[0][0], 一共用到了两个坐标索引,所以这个数组的维度是2维。
直观的说数组的维度就是所有基本元素左边 [ 个数的最大值。而每个坐标索引可取的值是有范围的,比如这里两个索引都只能取 0 和 1。维度与坐标值范围就组成了多维数组的 shape 属性,它是一个元组,长度代表了维度,而元组的每一个值代表了一个坐标索引可取的值个数,所以将 shape 的所有值乘起来就可以算出多维数组元素的个数。就如举例中的两个例子一个是2*2的数组,而另一个是一个3*3的数组。
轴
轴这个概念可以说是我第一次看到这个概念,在学习线性代数的时候,貌似也没有听过(大雾)。理解numpy中的轴的概念对我们接下来理解numpy中的转置transpose有着至关重要的作用。
如果我们直接说轴这个概念,童鞋们可能会比较迷茫,我们先来说一个和它非常相似的概念—坐标轴。n 维空间里有 n 个坐标轴,并且坐标轴互相垂直,每一个点相对于一条坐标轴都有唯一的一个坐标值。对同一条坐标轴来说,坐标值相同的点在同一个 n-1 维的“平面”上。任意取一个“平面”,我们就能定义“同一个坐标轴上的点”,这些点在“平面”上的投影相同,同一个坐标轴上的点组成的线是与坐标轴平行的。而所谓的延轴计算实际上是降维的过程,同一个坐标轴上的点合并成一个点,这样n维空间就变成了 n-1 维空间。例子
>> data2
array([[[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]],
[[12, 13, 14, 15],
[16, 17, 18, 19],
[20, 21, 22, 23]]])
>> data2.shape
(2L, 3L, 4L)
这里会常常提到这样的一个例子,这个数组我们该如何称呼它呢?2行3列4个平面。这其实就和我们上面所描述的坐标轴的概念十分的接近。如果你喜欢这样的说法也是可以的。
看完了坐标轴,下面我们来说说轴,如果还是有些问题的童鞋可以参考一下下面的理解。要理解它,我们可以先使用一下它,并且观察一下它是如何进行操作的。我们用最简单的累加来进行一下操作。代码如下
data2.sum(axis=0)
Out[49]:
array([[12, 14, 16, 18],
[20, 22, 24, 26],
[28, 30, 32, 34]])
data2
Out[50]:
array([[[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]],
[[12, 13, 14, 15],
[16, 17, 18, 19],
[20, 21, 22, 23]]])
data2.sum(axis=1)
Out[51]:
array([[12, 15, 18, 21],
[48, 51, 54, 57]])
data2.sum(axis=2)
Out[52]:
array([[ 6, 22, 38],
[54, 70, 86]])

红线框代表的是以轴为0相加的情况,而黄线则是轴为1,蓝线自不必多说就是轴为2的情况。
具体到 numpy 中的多维数组来说,轴即是元素坐标的索引。比如,第0轴即是第1个索引,延0轴计算就是去掉坐标中的第一个索引。过程就是
- 遍历其他索引的所有可能组合
- 取出一个组合,保持值不变,遍历第一个索引所有可能值
- 根据索引可以获得了同一个轴上的所有元素
- 对他们进行计算得到最后的元素
- 所有组合的最后结果组到一起就是最后的 n-1 维数组,所以如果一个多维数组的 shape 是 (a1, a2, a3, a4), 那么延轴0计算最后的数组shape 是 (a2, a3, a4), 延轴1计算最后的数组shape是 (a1, a3, a4)。
网上找到了两张图,比较直观
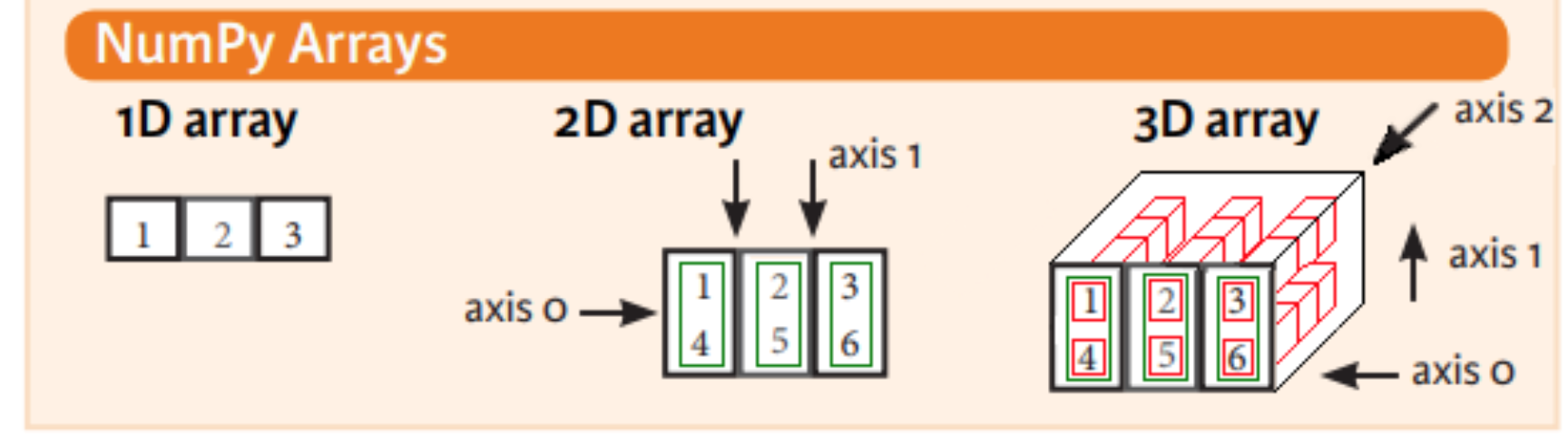
平时处理的都是二维的数据,所以大多数场景下使用的时死记硬背。把axis=1记作行,把axis=0记作列。(在pandas中,针对二维数据可以将axis=1写成axis=’columns’,将axis=0写成axis=’rows’)
另外一种比较好理解的记忆方式是将轴数记忆为中括号的嵌套深度,最外层的为0,每增加一层加1

Shape元组对应的下标及为“轴”。shape 中的各个数就是对应 axis 的元素个数。
ndarray的矩阵运算
ndarray的维数转换
最后我们来说一下numpy的transpose这个参数。这个参数是我们在基于理解了轴,维度等情况下对多维数组进行的一个重要的操作,不过这个理解起来倒确实有些令人头疼。
首先我们对矩阵的维度进行编号,上述矩阵有三个维度(假设),则编号分别为0,1,2,而transpose函数的参数输入就是基于这个编号的,如果我们调用transpose(0,1,2),那么矩阵将不发生变化,如果我们不输入参数,直接调用transpose(),其效果就是将矩阵进行转置,起作用等价与transpose(2,1,0)。
arr3d = np.random.rand(2,3,4) # 2x3x4 数组,2对应0,3对应1,4对应3 print(arr3d) print(arr3d.transpose((1,0,2))) # 根据维度编号,转为为 3x2x4 数组
 Shmily's Blog
Shmily's Blog